Traditionally, most of the multi-class classification problems (i.e. problems where you want to predict where a given sample falls into, from a set of possible results) focus on a small number of possible predictions. For most purposes, whether teaching data science or dealing with a lot of real-life scenarios, this would be ok. These kinds of scenarios include the typical examples of classifying a given e-mail as Spam/Legitimate, classifying an image of a skin mole as being a melanoma/normal, or the music genre of some song playing on the radio.
But what if, for example, we want to be more granular, and are trying to predict the artist playing the music? There are simply too many of them to consider at once – but at the same time, we know that there are some shared characteristics among them and that we can group them together based on those characteristics and exploit their relationships. Other more specific examples of these scenarios would be:
– Predicting a single, discrete diagnosis, from within the set of over 70.000 cases described and catalogued in the extended versions of the ICD-10 system (a medical classification system by the World Health Organization used worldwide). Due to the very nature of the diagnosis process, the system is actually hierarchically organized, so that we can start by the top level and consider only around 20 major categories – and go from there, following a narrowing path of prediction.
– Similar to the ICD-10 example, we could be interested instead in trying to predict certain adverse events related to pharmaceutical compounds described in the MedDRA. Instead of going straight to the prediction of the over 70.000 terms included in the lowest level, we can follow a similar strategy as above and initial predict only the bodily system (say Cardiovascular) and follow from there until we reach a highly specific event such as Supraventricular Tachycardia.
Flat And Hierarchical Classification Approach
The first approach is usually termed a flat classification approach, meaning that there is no inherent hierarchy between the possible categories the data can belong to (or we chose to ignore it). The second type of scenario involves considering a different strategy: hierarchically organizing the classes, creating a tree or DAG (Directed Acyclic Graph) of categories, exploiting the information on relationships among them. Although there are different types of hierarchical classification approaches, the difference between both modes of reasoning and analysing are particularly easy to understand in these illustrations, taken from a great review on the subject by Silla and Freitas (2011)1:
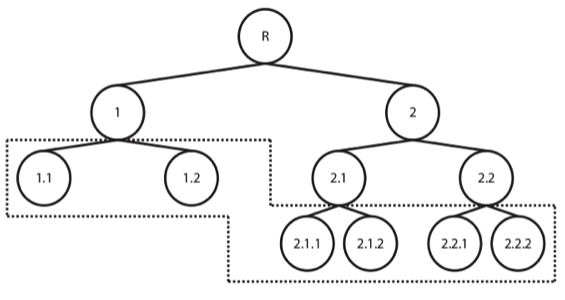
Figure 1: Flat classification approach
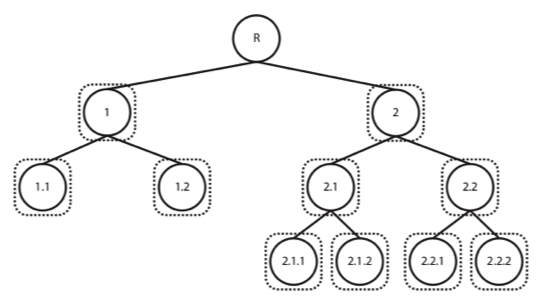
Figure 2: Hierarchical classification approach – using 1 classifier per node
As can be seen from the figures, the flat approach is the most commonly described, were our categories of interest are the down-most level of description possible. In the second method illustrated, however, we consider that each category can be grouped together with similar categories, creating meta-classes, which in turn can be grouped again until we reach the root level (set containing all data).
While in the first case we train either a single classifier to predict all of the available classes or one classifier per category (1 vs All), in the latter we take what is called a top-down approach, training a classifier per level (or node) of the tree (again, although this is not the only hierarchical approach, it is definitely the most widely used and the one we’ve selected for our problem at hands), where a given decision will lead us down a different classification path.
Let’s Go Back to Our Music Example
- we start first by training a classifier to predict, let’s say, the genre of the music (Death Metal) and then,
- we train another classifier to predict, for example, the nationality of the band (Swedish), and then
- we can have a classifier trained on predicting existing bands within that sub-group (Arch Enemy, At the Gates, …)
Now, the fact that we are chaining classifiers can be extremely helpful in breaking down the problem and increasing overall performance. In one particular case being explored in our DataOps platform, with roughly 30k samples distributed over more than 4 thousand classes (unevenly distributed), a flat approach gave us the ability to consider a small (in the 10’s) number of classes while keeping acceptable levels of confidence. By breaking the approach into a 2-level hierarchical approach we are up to the 100’s of predictable classes, and the inclusion of a 3rd level is on its way to further increase this number.
Now, why can’t we just go on including multiple levels of prediction until we reach a detailed coverage of the whole dataset? Well, no approach is perfect, and hierarchical classification has its own problems, mostly around two main issues: error propagation and overfitting.
The first problem arises from the fact that we are chaining decisions and thus propagating the error to each subsequent step. That is, when predicting the genre of the music, it’s inevitable to have a degree of error associated with it, which we will take with us when we go on to predict the nationality. This happens because we are dealing with events/decisions, which depend on past steps.
This structure of analysis forces us to, on one hand, find a more apt way to measure performance (traditional metrics from flat approaches tend to fall short) and, on the other, to decide how to constrain the error propagation. There are several options for both needs: in the first case, some combined performances measures have been developed, like hierarchical F-scores. In the second case, the simplest of approaches consists in blocking, where entering the next step of prediction only happens if we achieve a sufficient confidence in the prediction of the previous node. Of course, this will lead to cases where our predictions aren’t as informative as possible (i.e., predicting only a higher node of the tree/dag), but they won’t be as error-prone.
The second problem is actually common to all types of classification problems, but it’s particularly pressing in the hierarchical case. While we navigate our hierarchical structure, we are by definition reducing the amount of data present in each step (as a consequence of focusing only on a subset of potential outcomes). The problem comes from the fact that whenever we start training classifiers based on a small dataset (i.e, with a small number of observations), the probability increases that our statistical modelling of that category becomes very strict since each observation is a major contribution to it, which will lead to poor generalization performance. That is, our classifier will be very good at predicting those very specific examples but will fail on other slightly differing observations. Different classifiers and tuning parameters will lead to more or less proneness to overfitting, but the major rule to keep in mind is that we should set a minimum threshold of observations to consider when dealing with a new node, thus guaranteeing that we actually have enough data to learn something from it. Going back to our musical example, if we only have one Swedish Death Metal entry in our dataset (which would be a shame), we are necessarily not going to be good at predicting that category.
This problem is particularly pressing in some fields, namely healthcare. When considering a system like the above-mentioned ICD-10, we need to consider that the distribution of diagnosis in the population actually follows a pattern loosely called long tail. That is, the majority of the observations actually come from a minority of classes. In practical terms, this means that we are going to be able to build a hierarchical model that accounts for the small subset of the most commonly occurring codes in the healthcare system and thus covering, say, 90% of the patients, but by definition we will have limited access to the larger number of diagnosis which rarely happens. This means that, in practice, if we want to be comprehensive in our predictive approach, we will need to tackle these cases by taking, for example, an explicit rule-based approach, or reverse engineer it if it is not present or if it is only implicit.
Overall, breaking our problem into smaller steps of prediction allowed us to drastically improve our prediction ability, although at the small cost of increasing the complexity of the project (and subsequently of the code base and supporting apps).
Stay tuned for further posts on how we are tackling ML (Machine Learning) challenges at John Snow Labs or schedule a call to know more!
Exploring advanced AI tools, such as generative AI in healthcare, alongside healthcare chatbot solutions, opens new possibilities in accurately classifying and predicting medical categories, supporting enhanced decision-making in patient care.
References
1 Silla, C.N. & Freitas, A.A. Data Min Knowl Disc (2011) 22: 31. https://doi.org/10.1007/s10618-010-0175-9





























